If math has ever made you feel like you're solving ancient alien riddles, you're not alone. But here’s the good news — GMAT Quant isn’t about being a human calculator. It’s about recognizing patterns, applying logic, and sometimes just knowing when to plug in a number and hope it behaves.
Among the various topics in the GMAT Quant section, Number Properties and Arithmetic are the true MVPs. According to data from GMAT Club, nearly 60% of Quant questions across practice exams and official tests fall under these two categories. That’s right — if Quant were a party, Number Properties and Arithmetic would be the ones hogging the mic and busting moves on the dance floor.
Why focus on these? Because mastering them means unlocking at least half the points in the section. And for anyone aiming for a 700+ score, this is non-negotiable. These topics test your understanding of the fundamentals — odd/even, primes, divisibility, fractions, ratios, percentages — and if that already sounds familiar, that’s because you learned it all back in school, probably before you knew how to properly microwave leftovers.
So whether you're brushing up on math after a decade-long break or you're fresh out of college wondering why prime numbers are still a thing — you’re in the right place. Let’s make sense of these concepts, crack some jokes, and most importantly, crack the GMAT Quant code.
Even and Odd Numbers
Short Notes
Understanding even and odd numbers is like understanding the basic rules of a game. If you know the rules, the game gets a lot easier! Here’s the breakdown:
- Even numbers are those divisible by 2, like 2,4,6,8 and so on. The moment you see a 2 at the end, it’s even.
- Odd numbers leave a little “leftover” when divided by 2, like 1,3,5,7 and so on. You can tell they're odd by their unpredictable behaviour (just like some of us on a Monday morning!).
The Law of Calculation:
- Addition/Subtraction:
- Even + Even = Even
- Odd + Odd = Even
- Even + Odd = Odd
- Multiplication:
- Even × Anything = Even
- Odd × Odd = Odd
Tips:
- When dealing with even and odd numbers in equations, think of it like a dance: they always have their partners, and if the rhythm is wrong (like even + odd), things get messy!
- Trick to Remember: Whenever you see an "even" number in a problem, mentally high-five yourself because it’s the easiest to work with.
Example with Step by Step Solution


Which of the following numbers is divisible by 6?
(A) 342
(B) 421
(C) 537
(D) 216
Solution:
A number is divisible by 6 if it is divisible by both 2 and 3.
- Divisibility by 2: A number is divisible by 2 if its last digit is even.
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is a multiple of 3.
Checking each option:
- 342: Last digit is 2 (even), Sum = 3+4+2 = 9 (divisible by 3) → Divisible by 6
- 421: Last digit is 1 (not even) → Not divisible by 6
- 537: Last digit is 7 (not even) → Not divisible by 6
- 216: Last digit is 6 (even) , Sum = 2+1+6 = 9 (divisible by 3) → Divisible by 6
Correct answers: (A) 342 and (D) 216
Divisibility Rules
Short Notes
The divisibility rules are like shortcuts in a maze—they help you find the fastest path to the answer! Let’s break down some key divisibility rules:
- Divisible by 2: A number is divisible by 2 if it ends in 0, 2, 4, 6, or 8 (the classic even-number rule).
- Divisible by 3: If the sum of the digits of a number is divisible by 3, then the number itself is divisible by 3.
- Divisible by 5: A number is divisible by 5 if it ends in either 0 or 5.
- Divisible by 7: For 7, just double the last digit, subtract it from the rest of the number, and if the result is divisible by 7, you’re golden!
The Law of Calculation:
- Divisibility rules simplify your life by eliminating options and saving time. Instead of manually dividing each number, these rules help you make quick decisions on what’s possible.
Tips:
- Visualize the process: As soon as you see a number, mentally check if it fits the divisibility rule. It’s like playing Sudoku—get good at checking and eliminating!
- Practice with a twist: Try making a game of divisibility—every time you spot a number divisible by 5, take a “math break” (or a dance break—your choice).
Example with Step by Step Solution
Which of the following numbers is divisible by 6?
(A) 342
(B) 421
(C) 537
(D) 216
Solution:
A number is divisible by 6 if it is divisible by both 2 and 3.
- Divisibility by 2: A number is divisible by 2 if its last digit is even.
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is a multiple of 3.
Checking each option:
- 342: Last digit is 2 (even) , Sum = 3+4+2 = 9 (divisible by 3) → Divisible by 6
- 421: Last digit is 1 (not even) → Not divisible by 6
- 537: Last digit is 7 (not even) → Not divisible by 6
- 216: Last digit is 6 (even) , Sum = 2+1+6 = 9 (divisible by 3) → Divisible by 6
Correct answers: (A) 342 and (D) 216
GCD and LCM
Short Notes
The Greatest Common Divisor (GCD) and Least Common Multiple (LCM) are your BFFs when it comes to solving problems with fractions, ratios, and shared schedules! Here’s the breakdown:
- GCD: It’s the largest number that divides two numbers. Imagine finding the biggest puzzle piece that fits into both puzzles (numbers).
- LCM: It’s the smallest number that both numbers divide into evenly. It’s like finding the smallest common ground where both numbers meet.
The Law of Calculation:
- GCD: Look for common factors between numbers, and pick the largest one.
- LCM: Multiply the highest powers of all prime factors of each number. It’s like collecting the best parts of each number and putting them together.
Tips:
- Trick to Remember GCD: Think of it as the “greatest” factor that works for both numbers. If a number can’t be evenly divided by both, it’s not in the club!
- LCM Tip: Keep your eyes peeled for multiples. If you’re hunting for an LCM, it’s like looking for a party where both numbers are invited.
Example with Step by Step Solution

Remainders and Modular Arithmetic
Short Notes
Remainders and modular arithmetic are like leftovers—what you get after you divide. When you divide a number by another, the remainder is what's left over. Modular arithmetic just gives you a shortcut to figure out those leftovers.
- For example, 37÷5=7 remainder 2, and we can say 37mod 5=237 \mod 5 = 2.
The Law of Calculation:
- Think of modular arithmetic as the art of “remainder math.” It’s all about how things divide up and what’s left behind. Remember to apply the "mod" as the remainder of division!
Tips:
- Fun Tip: Picture the remainder as a rebellious kid who doesn’t fit into the full group—he’s just "leftover," and you’re trying to figure out how much room is left!
- Practice Tip: Use modular arithmetic when you want to skip all that long division—just look for shortcuts! You'll become a remainder-solving ninja in no time.
Example with Step by Step Solution
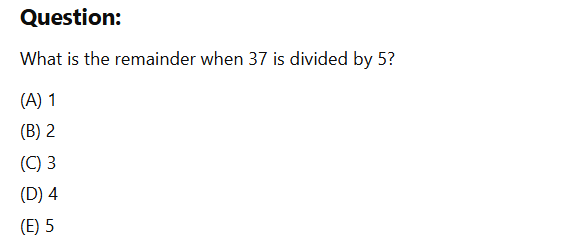
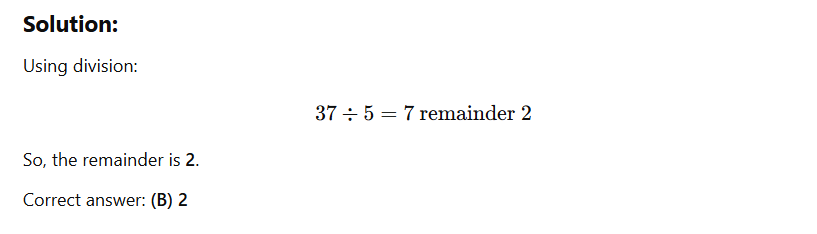
Conclusion:
Let’s face it — Number Properties and Arithmetic aren’t the flashiest topics. They're not the Beyoncé of the GMAT. But guess what? They’re the ones that make or break your score.
Think of them like the vegetables of Quant prep: maybe not exciting, but 100% necessary. And the best part? Once you get the hang of them, they’re not just manageable — they’re actually fun. There’s something oddly satisfying about figuring out that a number divisible by 3 and 4 is also divisible by 12, or realizing that plugging in 0, 1, or -1 can break a problem wide open like a piñata at a math nerd’s birthday party.
According to GMAC (Graduate Management Admission Council), the average GMAT Quant score is around 40 — but top business schools often admit candidates with scores above 47. That’s your target. And the way to get there? Master the basics, build confidence, and practice like you're preparing for a Quant-themed Olympics.
So take this as your sign: sharpen your mental pencil, power up that calculator you’re not allowed to use, and dive headfirst into the world of Number Properties and Arithmetic. You’ve got this — and if you ever feel stuck, just remember: every GMAT master was once a confused beginner who didn’t know what an integer was.