Let’s face it — numbers can be scary. For many GMAT aspirants, the phrase “solve for x” might as well be “face the dragon.” But here’s the truth: the GMAT Quant section isn’t out to get you — it’s just trying to measure how logically you can think under pressure (while the clock menacingly ticks away in the corner).
Now, when it comes to Rates, Ratios, and Percentages, you’re not just dealing with abstract math — you’re diving into the daily language of real life. Think about it:
Ever calculated how fast your battery dies while scrolling Instagram? That’s a rate.
Ever compared how much pizza your friend ate vs. you? That’s a ratio.
Ever bragged about saving 70% on that “totally necessary” Amazon cart? Yup, that’s a percentage.
Stat check: According to GMAC, about 50–60% of GMAT Quant problems involve topics like rates, ratios, percentages, and word problems — not directly, but often woven into Data Sufficiency or Problem Solving formats. (Source: GMAC Official Guide)
So, if you're looking to turn your fear of fractions into a friendship and turn those percentage problems into power plays — you're in the right place. This guide is here to help you laugh, learn, and level up your GMAT game, one number at a time. Let’s crunch it like it’s cardio!
What Are Rates?
At its core, a rate is a comparison between two different units. It’s like math’s way of saying, “How much of this per that?”
For example:
Speed is a rate: miles per hour (mph)
Typing speed is a rate: words per minute (wpm)
Productivity is a rate: tasks completed per hour
So if you’ve ever said, “I watched 3 Netflix episodes in 1 hour,” congratulations — you’re already doing rate problems.
Common Rate Problems
1. Speed = Distance ÷ Time
This classic formula pops up in questions about cars, trains, planes, or joggers in a park.
Example: If a car travels 180 miles in 3 hours, what’s its average speed?
Answer: 180/3=60 mph.
2. Work = Rate × Time
In GMAT-speak: How fast can a person or machine get the job done?
If someone paints a wall in 4 hours, their rate is 1/4 wall per hour.
Combine multiple workers = sum of their individual rates!
3. Unit Conversions
Convert miles to kilometers, minutes to seconds, etc. — especially when the question is trying to trip you up with mismatched units.
Average Rates vs. Combined Work Rates
Average Rates
Don’t just average the speeds!
If you drive to work at 30 mph and come back at 60 mph, your average isn’t 45 mph — it’s:
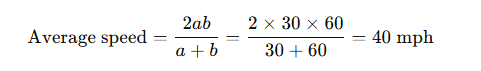
Combined Work Rates
If Person A can do a job in 3 hours and Person B in 6 hours, their combined rate is:
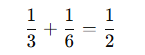
So together, they finish the job in 2 hours.
What is Ratios?
Ratios are just the comparison between two or more things, usually written in a form like a:b or a/b. This is essentially the law of proportions—what happens to one thing when another thing changes. It's like that time you mixed 3 parts juice to 2 parts water, and everything magically tasted perfect!
The Law of Calculation for Ratios
- If you have a ratio a:b and you’re asked to find the missing values, the general rule is:
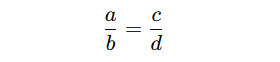
- Meaning: cross-multiply! So, if a:b = c:d, then a × d = b × c. Just like two slices of pizza being equally split between two friends—if you cross-multiply, you keep everything fair and square.
Tip:
When you get a ratio question, treat it like a recipe. If you're given ingredients (numbers), just mix them in the right proportion! Stay calm and remember: ratios aren’t as scary as they sound, they’re just math recipes waiting to be solved. Keep the proportions balanced, and you’ll be the pizza-maker of the GRE!
Example with Step by Step Solution
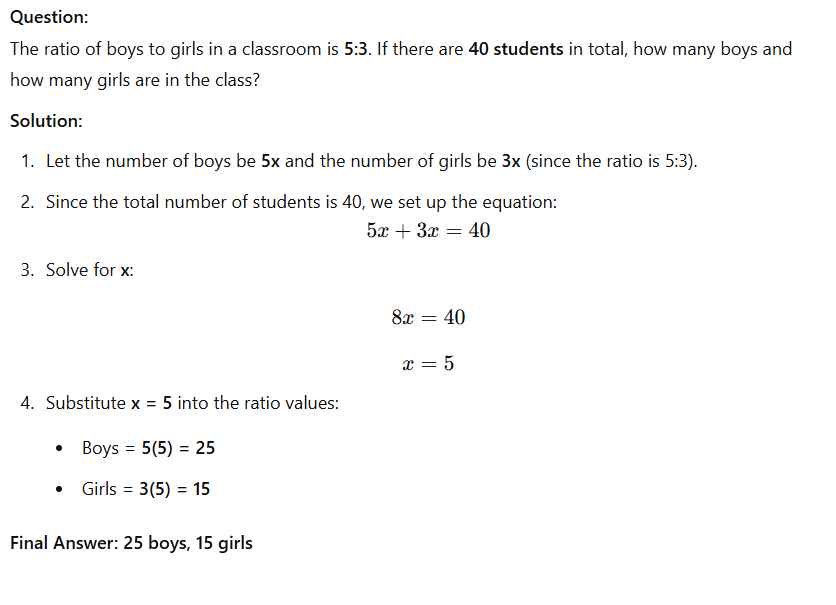
What Is a Percentage?
The word percentage comes from the Latin per centum, meaning “by the hundred.”
So when we say 40%, we really mean 40 out of 100, or simply:
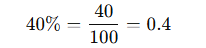
Percentages are used to compare quantities relative to 100, making them incredibly useful in everything from calculating discounts to measuring profit, loss, interest, population growth, and even exam scores.
Percentage Increase & Decrease
Percentage Increase Formula:
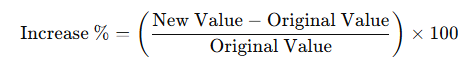
Percentage Decrease Formula:
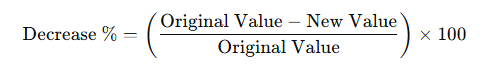
Successive Percentage Changes
When a value changes by a percentage more than once, you can’t just add or subtract the percentages. This is where most people mess up!
Formula:
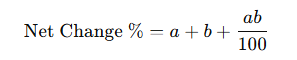
Where a and b are the first and second percentage changes.
Remember: If one is a decrease, make it negative in the formula.
Step-by-Step Example
Problem: A product’s price increases by 20% in the first year, and then decreases by 10% in the second year. What is the overall percentage change?
Step 1: Use the Net Change Formula
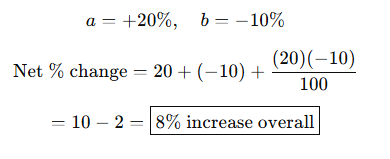
Step 2: Verify with Numbers

Sure! Here's a clear and concise comparison table highlighting the difference between Rates, Ratios, and Percentages:
Rates vs Ratios vs Percentages
| Feature | Rates | Ratios | Percentages |
|---|---|---|---|
| Definition | Comparison between two quantities with different units | Comparison between two quantities with the same or related units | A way to express a part per hundred |
| Format | A per B (e.g., km/hr, $/hour, tasks/minute) | A : B or A/B | A% = A/100 |
| Units | Always includes units (e.g., km/hour) | No units, or same units cancel out | Unitless (just a fraction or decimal × 100) |
| Used For | Speed, Work rate, Cost per item | Comparing quantities, mixing ingredients, parts to whole | Discounts, growth, change, comparison to 100 |
| GMAT Examples | Speed = Distance/Time, Work = Rate × Time | Mixing ratios, part-to-part comparisons | Percentage increase/decrease, successive change |
| Example | 60 miles per hour | 2:3 (e.g., boys to girls) | 25% discount on $100 = $25 |
Absolutely! Here's a detailed, reader-friendly section for your blog on Common Pitfalls and How to Avoid Them when dealing with Rates, Ratios, and Percentages in the GMAT Quant section — with examples and tips to help avoid traps.
Common Pitfalls and How to Avoid Them
1. Confusing Units in Rate Problems
Pitfall: Using mixed units (e.g., minutes with hours) without converting.
Example:
A car travels at 60 mph for 30 minutes. How far does it go?
Wrong answer: 60×30= 180 (You forgot to convert minutes to hours!)
Avoid It:
Always convert time to the same unit as the rate.
Correct: 60×(30/60)=30 miles
2. Adding Percentages Directly in Successive Changes
Pitfall: Assuming 20% increase followed by 10% decrease = 10% increase overall.
Why it's wrong: Percentage changes are not additive.
Avoid It:
Use the Net % Change Formula:
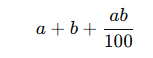
Or plug in 100 as a base to test. Always double-check!
3. Misreading Ratio Questions as Totals or Vice Versa
Pitfall: Thinking the ratio 2:3 means there are only 5 items.
Example:
If the ratio of cats to dogs is 2:3 and there are 15 dogs, how many cats?
Wrong: Cats = 2
Correct: Total parts = 2+3 = 5; 3 parts = 15 → 1 part = 5 → 2 parts = 10 cats
Avoid It:
Set up ratios with actual numbers using proportional relationships.
4. Forgetting What the Question Is Really Asking
Pitfall: Solving the problem correctly... then picking the wrong answer choice because you misunderstood what to solve for.
Example:
A question asks, “What is the percentage increase?” but you calculated the difference in values only.
Avoid It:
Underline or rewrite what the question is asking — is it the amount, the percentage, or the ratio?
Always re-read the final question line before choosing your answer.
5. Rushing Through “Easy” Questions
Pitfall: Thinking a rate or percentage question looks simple, skipping setup, and making a silly mistake.
Avoid It:
Even if the question looks easy, write out a small setup.
Use the rate triangle: Distance = Rate × Time
Use percent formulas: New = Original × (1 ± % change)
A few extra seconds could save several points!
Practice Problems with real time examples
Practice Question 1
If the price of gasoline increases by 25% and Ron intends to spend only 15% more on gasoline, by what percentage should he reduce the quantity of gasoline he buys?
Solution:
Let’s assume Ron initially buys 100 liters of gasoline at $1 per liter, so he spends $100.
New price per liter = $1 + 25% of $1 = $1.25
New budget = $100 + 15% of $100 = $115
New quantity = $115 / $1.25 = 92 liters
Reduction in quantity = 100 liters - 92 liters = 8 liters
Percentage reduction = (8 / 100) × 100% = 8%
Answer: 8%
Practice Question 2
In Mr. Smith’s class, what is the ratio of the number of boys to the number of girls?
Statements:
There are 3 times as many girls as boys in Mr. Smith’s class.
The number of boys is ¼ of the total number of students in the class.
Solution:
Let’s denote:
Number of boys = B
Number of girls = G
Total students = B + G
Statement 1: G = 3B ⇒ B:G = 1:3
Statement 2: B = ¼(B + G)
Multiply both sides by 4:
4B = B + G ⇒ 4B - B = G ⇒ 3B = G ⇒ B:G = 1:3
Both statements individually provide the same ratio.
Answer: Each statement alone is sufficient.
Practice Question 3
A product’s price increases by 20% in the first year and then decreases by 10% in the second year. What is the overall percentage change in price over the two years?
Solution:
Let’s assume the original price is $100.
After a 20% increase: $100 + 20% of $100 = $120
After a 10% decrease: $120 - 10% of $120 = $108
Overall change = $108 - $100 = $8 increase
Percentage change = ($8 / $100) × 100% = 8% increase
Answer: 8% increase
Practice Question 4
A train travels at a constant speed of 90 kilometers per hour. How many kilometers does it travel in 40 minutes?
Solution:
Convert 40 minutes to hours: 40 minutes = 40/60 = 2/3 hours
Distance = Speed × Time = 90 km/h × 2/3 h = 60 kilometers
Answer: 60 kilometers
Practice Question 5
Worker A can complete a task in 5 hours, and Worker B can complete the same task in 3 hours. How long will it take them to complete the task if they work together?
Solution:
Worker A’s rate = 1 task / 5 hours = 1/5
Worker B’s rate = 1 task / 3 hours = 1/3
Combined rate = 1/5 + 1/3 = (3 + 5) / 15 = 8/15
Time to complete one task together = 1 / (8/15) = 15/8 hours = 1 hour and 52.5 minutes
Answer: 1 hour and 52.5 minutes
Practice Question 6
A machine can produce 150 widgets in 5 hours. At this rate, how many widgets can it produce in 8 hours?
Solution:
Determine the rate of production:
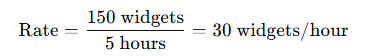
Calculate the number of widgets in 8 hours:
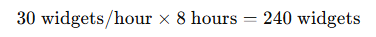
Answer: 240 widgets
Practice Question 7
In a class, the ratio of boys to girls is 3:2. If there are 15 boys, how many girls are there?
Solution:
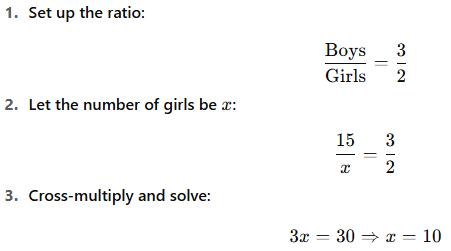
Answer: 10 girls
Practice Question 8
A product's price increased from $200 to $250. What is the percentage increase?
Solution:
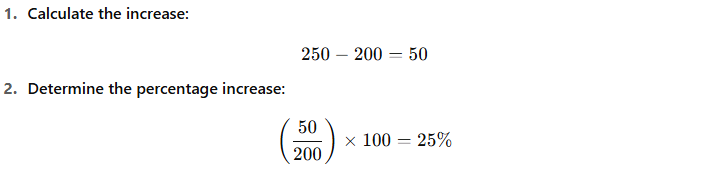
Answer: 25% increase
More Practice Question
A baseball team won 45 percent of the first 80 games it played. How many of the remaining 82 games will the Describe how ratios and proportions are tested on the GMAT Identify questions that involve ratios and proportions Apply the Kaplan Methods for Problem Solving and Data Sufficiency in questions that test ratios and proportions team have to win in order to have won exactly 50 percent of all the games it played?
(A) 36
(B) 45
(C) 50
(D) 55
At a certain university, the football program receives 4 times more funding than does the basketball program. Together, the football and basketball programs receive 3 times as much funding as do all other sports programs combined. What is the ratio of funding for the basketball program to funding for all other sports programs, not including the football program?
(A) 1:5
(B) 1:4
(C) 3:5
(D) 3:4
(E) 5:3
A movie buff stores movies on the internet and on her personal computer in a ratio of 7:2. If she purchases 6 new movies and downloads them to her personal computer, that ratio would change to 11:4. If she stores movies in no other locations, what was the original number of movies she owned before the purchase of new movies?
A) 22
B) 28
C) 77
D) 99
E) 105
Conclusion:
Congratulations — you made it through a jungle of rates that race, ratios that rumble, and percentages that perplex. If you're still standing, give yourself a high-five (and maybe a cookie — you’ve earned it).
The good news? These aren’t just math tricks for test day — they’re lifelong tools. You'll use them to negotiate salaries, calculate investments, or divide the bill at a fancy dinner without looking like you're decoding the Da Vinci Code.
Remember:
Don’t get overwhelmed — even the toughest problems break down into bite-sized logic.
Use strategies like plugging in numbers, drawing it out, or laughing at your mistakes (seriously, it's therapeutic).
And most importantly, practice like your future MBA depends on it — because it just might.
The average GMAT Quant score in recent years is around 40 out of 60, but a top MBA program often expects 45+. (Source: mba.com) Mastering core topics like these could be your ticket to standing out.
